| Acest site se adresează celor interesaţi de programare şi mai ales elevilor de la specializarea matematică-informatică. Site-ul se doreşte a fi o culegere online de probleme de informatică, explicate şi rezolvate. Problemele sunt organizate pe anii de studiu şi pe capitole. Problemele specifice claselor IX-XI sunt rezolvate folosind C/C++, iar pentru clasa a XII-a folosind C# (Visual Studio 2010-2017). | Site-ul va fi actualizat permanent, de aceea va rog sa urmăriţi problemele noi. O atenţie deosebită este acordată pregătirii examenului de bacalaureat. Veţi găsi aici rezolvate probleme din variantele propuse in anul 2009, precum si dintre cele de la examenele din 2010-2018. Pentru pregătirea examenului de obţinere a atestatului profesional la informatică găsiţi aici modele de lucrări de atestat. Pentru pregătirea examenului de competenţe digitale: variante 2011-2015 . |
Cele mai noi probleme adăugate
| #885. [2020-10-26 - 08:30:22] Exemplu de indexator cu parametru string (pentru cautarea unui elev dupa nume si prenume). | Rezolvare |
| #884. [2020-01-20 - 13:23:49] Se dă un graf neorientat cu n (n<=100) vârfuri si m muchii prin lista muchiilor. Afisați toate subgrafurile pe care le are. Fiecare subgraf va fi afișat astfel: - vârfurile lui - matricea de adiacență Exemplu: graf.in 3 2 1 2 1 3 graf.out Varfurile subgrafului: 1 Matricea de adiacenta: 0 0 0 0 0 0 0 0 0 Varfurile subgrafului: 1 2 Matricea de adiacenta: 0 1 0 1 0 0 0 0 0 Varfurile subgrafului: 1 2 3 Matricea de adiacenta: 0 1 1 1 0 0 1 0 0 Varfurile subgrafului: 1 3 Matricea de adiacenta: 0 0 1 0 0 0 1 0 0 Varfurile subgrafului: 2 Matricea de adiacenta: 0 0 0 0 0 0 0 0 0 Varfurile subgrafului: 2 3 Matricea de adiacenta: 0 0 0 0 0 0 0 0 0 Varfurile subgrafului: 3 Matricea de adiacenta: 0 0 0 0 0 0 0 0 0 | Rezolvare |
| #883. [2020-01-20 - 11:23:43] Se dau două grafuri neorientate G1 și G2 cu n (n<=100) vârfuri și m1, respectiv m2 muchii prin listele muchiilor, în două fișiere graf1.in, respectiv graf2.in. Verificați dacă unul dintre ele este graf parțial al celuilalt. Se va preciza dacă G1 este graf parțial al lui G2, dacă G2 este graf parțial al lui G1 sau NU dacă niciunul dintre ele este graf parțial al celuilalt. Exemplu: graf1.in 5 2 1 4 1 3 graf2.in 5 5 1 4 1 3 3 5 4 5 2 5 graf.out G1 este graf partial al lui G2 | Rezolvare |
| #882. [2020-01-20 - 10:45:58] Se dă un graf neorientat cu n (n<=100) vârfuri si m muchii prin lista muchiilor. Afisați toate grafurile parțiale pe care le are. Fiecare graf parțial va fi afișat astfel: - numărul lui de ordine (al câtelea a fost generat) - lista munchiilor lui - matricea de adiacență Exemplu: graf.in 4 2 1 4 1 3 graf.out Graful partial numarul 1: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Graful partial numarul 2: 1 4 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 Graful partial numarul 3: 1 4 1 3 0 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0 Graful partial numarul 4: 1 3 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 | Rezolvare |
| #881. [2019-10-28 - 13:19:16] Realizați în C# un program care să permită alegerea unui fișier care că conțină informații despre n bancnote (valoare si număr avut la dispoziție) și o sumă de bani S. Programul va afișa o modalitatea de plată exactă a sumei S folosind cel puțin câte o bancnotă de fiecare fel dintre cele n. |  | Rezolvare |
| #880. [2019-10-28 - 10:45:22] Realizați în C# un program care să permită alegerea unui fișier care că conțină informații despre n cuburi (latură și culoare) ca mai jos: 9 4 Red 2 Red 1 Green 4 Blue 1 Blue 3 Yellow 5 Pink 1 Red 6 Black Programul va desena cele n cuburi ca pătrate de culoarea dată și respectând dimensiunile, apoi va desena cel mai inalt turn care se poate forma cu cuburile date respectând regula că un cub poate fi pus peste un altul dacă are culoare diferită și latură mai mică. | 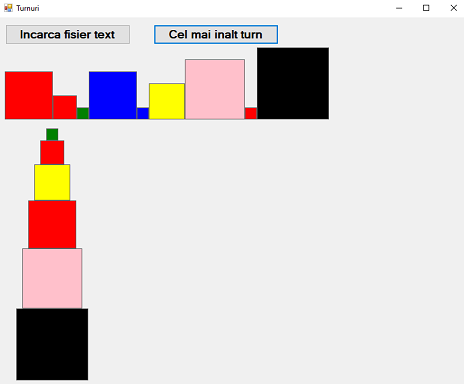 | Rezolvare |
| #879. [2019-10-28 - 10:31:11] Realizați în C# un program care să citească din fisierul traseucal.txt dimensiunile n și m ale unei table de șah în care sunt codificate cu 0 pozițiile libere și cu 1 cele ocupate. Să se afișeze un traseu pe care un cal poate ajunge din colțul stânga-sus (1,1) în colțul dreapta-jos (n,m) mergând doar pe poziții libere și fără să treacă de două ori prin aceeași poziție. (vezi Traseu cal). | 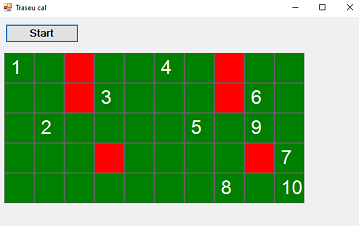 | Rezolvare |
| #878. [2019-05-28 - 16:27:09] Realizați în C# un program care să permită crearea unei table de dimensiune n*n de tipul unei table de sah care să conțină n*n butoane. Pe fiecare buton să se scrie linia și coloana pe care se află, iar la click pe el să fie scrise într-un MessageBox linia și coloana pe care se află. |  | Rezolvare |
| #877. [2019-05-14 - 17:05:08] Realizați în C# un program care să permită navigarea pe internet folosind controlul WebBrowser. Realizați următoarele operații: - Back - Forward - Memorare automată a istoricului (folosind un fisier txt), precum și posibilitatea stergerii unei adrese din istoric, a tututor adreselor și ordonarea alfaberică a adreselor din istoric - Posibilitatea salvării adreselor favorite (folosind un fisier txt), precum și posibilitatea stergerii unei adrese din favoritea tututor adreselor favorite și ordonarea alfaberică a adreselor favorite | 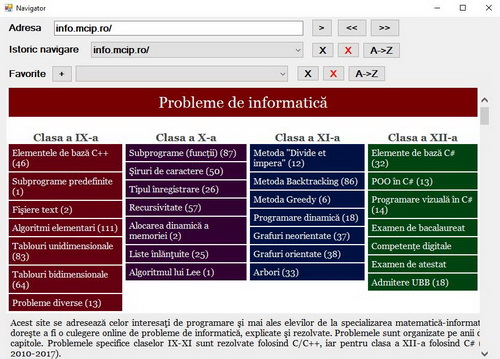 | Rezolvare |
| #876. [2018-12-12 - 12:15:59] Realizați în C# un editor de fișiere RTF care să permită alegerea următoarelor operații dintr-un meniu: a) Fisier - Nou - Deschide - Salvare - Salvare ca... - Iesire b) Editare - Copiere - Taiere - Lipire - Selectare totala c) Formatare - Font - Culoare d) Aliniere - Stanga - Dreapta - Centru Adăugați o bara de instrumente cu operațiile: Nou, Deschide, Salvare, Copiere, Taiere și Lipire. | 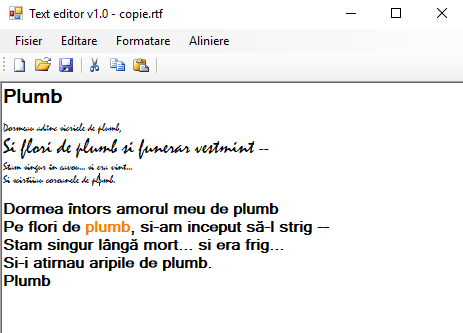 | Rezolvare |
| #875. [2018-12-12 - 11:36:23] Realizați în C# o aplicație care să ilustreze printr-o animație modul de funcționare a algoritmului fill pentru rezolvarea problemei Fill de pe pbinfo.ro. Adăugați codul sursa C# si C++. | 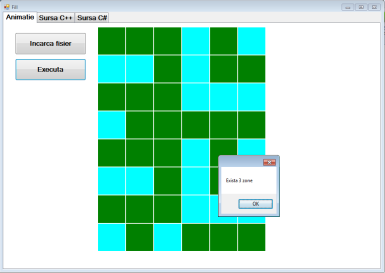 | Rezolvare |
| #874. [2018-12-11 - 17:19:53] Se dă un număr natural s cu cel mult 9 cifre. Afișaţi, în ordine lexicografică, toate modalităţile de a-l scrie pe s ca produs de divizori proprii distincți ai lui s. Exemplu: 30 poate fi scris in următoarele moduri: 2 3 5 2 15 3 10 5 6 | Rezolvare |
| #873. [2018-12-11 - 17:08:46] 2017 - Sesiunea iunie-iulie - Subiectul III - Problema 4 | Rezolvare |
| #872. [2018-12-11 - 17:01:50] 2018 - Sesiunea iunie-iulie - Subiectul II - Problema 5 | Rezolvare |
| #871. [2018-12-10 - 10:32:11] Se citește un număr natural n. Afișați toate tripletele de numere naturale x, y, z (1<x<y<z<n) care sunt divizori ai lui n și care au proprietatea că x+y+z=n. Programul va afișa pe ecran pe rânduri separate câte un triplet conform cerinței, numerele din triplet fiind in ordine strict crescatoare și separate prin cate un spațiu. Dacă nu există nici un astfel de triplet, atunci se va afișa pe ecran nu exista. Exemple: Pentru n=24 se obtin 4 8 12. Pentreu n=20 se afiseaza nu exista. | Rezolvare |
| #870. [2018-12-10 - 10:20:05] Realizați în C# o aplicație care să ilustreze printr-o animație modul de funcționare a algoritmului lui Lee pentru rezolvarea problemei Roboti de pe pbinfo.ro. Adăugați informații preluate pe internet (youtube). | 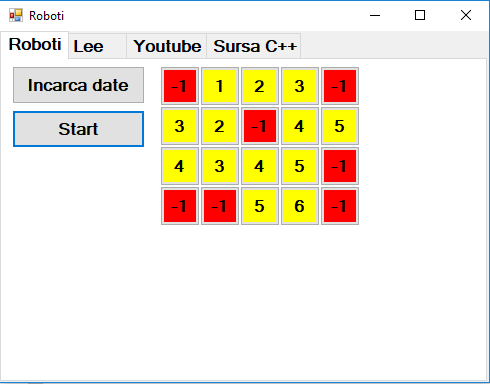 | Rezolvare |
| #869. [2018-11-08 - 11:45:42] Realizati in C# jocul XO. |  | Rezolvare |
| #868. [2018-08-03 - 19:34:32] Se citesc două numere naturale a și b (a mai mic decât b) având cel mult 9 cifre fiecare. Afișați câte numere din intervalul [a,b] au exact 3 divizori. Exemplu: În intervalul [11,50] numerele care au exact 3 divizori sunt 25 și 49, deci se va afișa 2. | Rezolvare |
| #867. [2018-08-03 - 19:25:16] Creați o aplicație care să realizeze următoarele: - folosind radiobutton-uri să permită alegerea unei figuri (punct, segment, cerc disc, pătrat, pătrat plin, dreptunghi, dreptunghi plin, poligon, poligon plin) - folosind un picturebox și un colordialog să permită alegerea ueni culori - pe un picturebox cu click stânga să se deseneze figura aleasă cu culoarea aleasă. Dimesiunile figurilor se vor stabili folosind un numericupdown pentru cerc si pătrat (inclusiv pline), vârfurile segmentului cu două clickuri, pentru dreptunghi (si plin) cu două clickuri pentru vârfurile opuse, iar pentru poligon (și plin) se vor plasa vârfurile cu click și cu dublu-click se va termina desenul. | 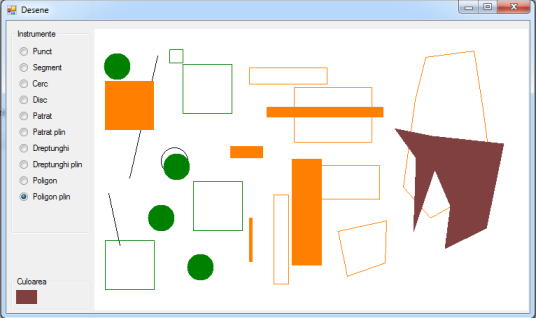 | Rezolvare |
| #866. [2018-08-03 - 19:09:33] Creați o aplicație care să conțină un un meniu cu două opținuni: Desene și Culori. Meniul Desene permite alegerea unei figuri dintre următoarele: punct, cerc, pătrat, disc și pătrat plin, iar opțiunea Culori permite alegerea unei culori de desenare. De asemenea, aplicația să conțină un picturebox pe care la click stânga să se deseneze în pozitia mouse-ului figura aleasă desenată cu culoarea aleasă. | 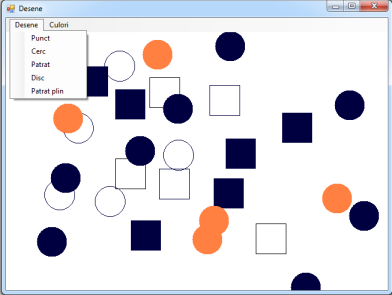 | Rezolvare |
27 apr 2024
Site-ul conține 884 de probleme rezolvate
Copyright © 2009-2018 Muresan Vasile Ciprian