Arbori
| #831. [2017-05-10 - 10:18:51] Se da o expresie aritmetica in forma poloneza prefixata. Expresia este formata din operatorii + - / * %, iar operanzii sunt litere mici. Afisati expresia in forma normala (infixata) si in forma postfixata. Exemplu: expresie.in -*bb**4ac expresie.out ((b*b)-((4*a)*c)) bb*4a*c*- | Rezolvare |
| #830. [2017-05-10 - 10:12:56] Se da un arbore cu radacina cu n varfuri (n<=100) prin vectorul de tati. a) Sa se determine daca este arbore binar si, in caz afirmativ, sa se afiseze vectorii S si D (consideram fiul stang < fiul drept) b) Daca raspunsul de la a este negativ, sa se determine daca prin schimbarea radacinii, arborele poate deveni binar. Exemplul 1: arbore.in 7 6 6 6 3 3 0 3 arbore.out NU NU Exemplul 2: arbore.in 6 6 6 6 3 3 0 arbore.out NU DA Exemplul 3: arbore.in 6 0 6 6 3 3 1 arbore.out DA 6 0 0 0 4 5 0 0 0 0 2 3 | Rezolvare |
| #829. [2017-05-10 - 10:05:53] Din fisierul graf.in se citeste un numar natural n (n<=100) si apoi muchiile unui graf neorientat conex cu n varfuri. Construiti un arbore partial al grafului dat si afisati in fisierul arbore.out vectorul de tati a acestui arbore avand radacina in varful 1. Se poate afisa vectorul de tati al oricarui arbore partial cu radacina in varful 1. exemplu: graf.in 5 1 2 1 3 1 4 2 3 2 4 2 5 3 4 3 5 4 5 arbore.out 0 1 1 1 2 | Rezolvare |
| #601. [2014-05-26 - 23:18:07] Se dau in fisiereul date.in numerele n, p si q unde n este numarul de noduri ale unui arbore iar p si q sunt noduri din arbore. Apoi se citeste vectorul de tati prin care este reprezentat arborele. Afisati lantul elementar de la varful p la varful q. Exemplu: date.in 7 2 5 4 1 7 0 7 7 1 date.out 2 1 7 5 | Rezolvare |
| #600. [2014-05-26 - 23:07:41] Intr-o firma sunt n angajati, numerotati de la 1 la n, fiecare angajat avand un singur sef direct, cu exceptia directorului, care nu are sef. Ierarhia firmei este data printr-un vector de tip tata. Fiecare angajat al firmei are un salariu dat printr-un numar natural. Angajatii si seful sunt recompensati astfel: castigul fiecarui salariat este egal cu salariul sau la care se adauga media aritmetica a castigurilor subordonatilor sai directi. Media aritmetica se rotunjeste prin adaos la un numar intreg (de exemplu 5.33 se rotunjeste la 6). Angajatii care nu au subordonati directi castiga doar salariul. Calculati care este castigul directorului firmei. Exemplu: firma.in 8 (numarul de angajati) 4 3 0 3 2 1 2 1 (vectorul tata) 2 6 4 3 7 3 1 5 (salariul fiecarui angajat) firma.out 14 | Rezolvare |
| #595. [2014-05-15 - 10:16:37] Se da un arbore cu n varfuri (cel mult 99) prin vectorul de tati. Folosind algoritmul asemanator cu algoritmul Roy-Floyd, determinati si afisati cel mai lung lant elementar din arborele citit. Exemplu: date.in 8 2 0 2 5 2 5 3 7 date.out 4 5 2 3 7 8 | Rezolvare |
| #594. [2014-05-15 - 10:01:20] In fisierul countsub.in se da un arbore binar cu n varfuri (cel mult 1000) prin vectorii S si D (pentru fiecare varf se precizeaza fiul stang si apoi cel drept). Sa se calculeze si sa se afiseze numarul de nivele ale arborelui si apoi cate varfuri se afla pe fiecare nivel. Exemplu: countsub.in 6 3 5 0 6 0 0 1 2 0 0 0 0 countsub.out 3 1 2 3 | Rezolvare |
| #593. [2014-05-15 - 09:55:41] In fisierul countsub.in se da un arbore binar cu n varfuri (cel mult 1000) prin vectorii S si D (pentru fiecare varf se precizeaza fiul stang si apoi cel drept). Sa se calculeze si sa se afiseze pentru fiecare varf v numarul de varfuri din subarborele care il are pe v ca radacina. Exemplu: countsub.in 6 3 5 0 6 0 0 1 2 0 0 0 0 countsub.out 3 2 1 6 1 1 | Rezolvare |
| #474. [2013-05-22 - 09:36:13] Se dau doi arbori cu radacina prin doi vectori de tip tata. Determinati daca cei doi arbori cu radacina reprezinta acelasi arbore (difera doar in urma alegerii radacinilor diferite) Exemplu: date.in 5 0 1 1 2 2 3 1 0 2 2 date.out da | Rezolvare |
| #473. [2013-05-22 - 09:24:03] Se da un arbore cu n noduri prin vectorul de referinte de tip tata. Sa se determine daca arborele poate fi reprezentat ca un lant. Exemple: n=6 T=0 1 1 2 3 2 raspunsul este nu n=6 t=0 1 1 2 3 5 raspunsul este da | Rezolvare |
| #470. [2013-05-16 - 13:32:19] Se da un numar natural n. Construiti un arbore binar complet cu varfurile 1,2...n astfel incat in urma parcurgerii pe nivele sa fie afisate valorile 1,2...n. Se vor afisa vectorii S si D. Exemplu n=8 S=2 4 6 8 0 0 0 0 0 D=3 5 7 9 0 0 0 0 0 | Rezolvare |
| #469. [2013-05-16 - 13:22:22] Se da un arbore binar cu n varfuri prin vectorii S si D. Stabiliti daca este plin, sau complet, sau nici unul dintre cazuri. Exemple: 7 2 3 4 5 5 6 0 0 0 0 0 0 0 0 plin 6 2 3 4 5 6 0 0 0 0 0 0 0 complet | Rezolvare |
| #468. [2013-05-16 - 12:45:55] Se da o expresie aritmetica in forma poloneza prefixata. Expresia este formata din operatorii + - / * %, iar operanzii sunt dintr-un singur caracter. Construiti arborele binat asociat expresiei citite si afisati expresia in forma normala (infixata). Exemplu: /-+*5314+27 in forma normala este (((5*3)+1)-4)/(2+7) | Rezolvare |
| #467. [2013-05-15 - 11:51:58] Se citeste un vector A cu n elemente numere intregi. Plasati indicii 1,2...n intr-un arbore binar astfel incat in urma parcurgerii in inordine a aceastuia sa se afiseze vectorul A sortat crescator. Arborele binar va fi reprezentat prin vectorii S si D. Exemplu: n=7 A=3 4 1 2 9 0 6 Vectorii S si D rezultati sunt: S=3 0 6 0 7 0 0 D=2 5 4 0 0 0 0 iar vectorul A sortat: A=0 1 2 3 4 6 9 | Rezolvare |
| #465. [2013-05-10 - 09:42:27] Se da un arbore binar cu n noduri prin vectorii de descendenti S si D. Afisati pe randuri separate: - frunzele arborelui - varfurile cu un singur descendent direct - varfurile cu doi descendenti directi Exemplu: date.in 12 2 3 4 5 0 6 7 8 0 9 10 11 0 0 0 0 0 0 0 0 0 12 0 0 date.out frunzele: 7 8 9 10 12 varfurile cu un singur descendent: 3 5 11 varfurile cu doi descendenti: 1 2 4 6 | Rezolvare |
| #464. [2013-05-10 - 09:26:08] Se da un arbore binar cu n noduri prin vectorii T si P (reprezentarea cu legaturi ascendente de tip tata si respectiv pozitia descendentului: -1 pentru stanga, 1 pentru dreapta). Afisati vectorii de descendenti S si D. Exemplu: date.in 12 0 1 1 2 2 3 4 4 5 6 6 11 (T) 0 -1 1 -1 1 1 -1 1 1 -1 1 1 (P) date.out 2 4 0 7 0 10 0 0 0 0 0 0 (S) 3 5 6 8 9 11 0 0 0 0 12 0 (D) | Rezolvare |
| #463. [2013-05-10 - 09:18:19] Se da un arbore binar cu n noduri prin vectorii de descendenti S si D. Afisati vectorii T si P (reprezentarea cu legaturi ascendente de tip tata si respectiv pozitia descendentului: -1 pentru stanga, 1 pentru dreapta). Exemplu: date.in 12 2 3 4 5 0 6 7 8 0 9 10 11 0 0 0 0 0 0 0 0 0 12 0 0 date.out 0 1 1 2 2 3 4 4 5 6 6 11 (T) 0 -1 1 -1 1 1 -1 1 1 -1 1 1 (P) | Rezolvare |
| #462. [2013-05-09 - 13:49:56] Se citeste un numar natural n. Construiti un arbore cu proprietatea ca fiecare varf are numarul de descendenti directi cu 1 mai mare decat nivelul pe care se afla. Exceptie fac frunzele si nodul pentru care se termina cele n varfuri. Astfel, radacina (aflata pe nivelul 0) are un singur descendent direct, varful de pe nivelul 1 are 2, cele de pe nivelul 2 au cate trei, etc. Arborele va fi reprezetat prin vectorul legaturilor de tip tata. Exemplu: n=15 Vectorul tata: 0 1 2 2 3 3 3 4 4 4 5 5 5 5 6 | Rezolvare |
| #461. [2013-05-10 - 12:25:19] Se da un arbore cu n varfuri avand muchiile etichetate cu costuri numere naturale. Calculati costul intre oricare doua varfuri ale arborelui. Exemplu: date.in 5 (n) 1 2 4 (i j cost) 1 3 5 2 4 6 4 5 1 date.out 0 4 5 10 11 4 0 9 6 7 5 9 0 15 16 10 6 15 0 1 11 7 16 1 0 | Rezolvare |
| #457. [2013-05-08 - 08:33:35] Se da un arbore prin vectorul de tip tata. Calculati si afisati distante dintre oricare doua varfuri ale arborelui sub forma unei matrici. Distanta dintre doua varfuri este egala cu lungimea lantului care le uneste. Exemplu: date.in 6 2 0 2 1 3 1 date.out 0 1 2 1 3 1 1 0 1 2 2 2 2 1 0 3 1 3 1 2 3 0 4 2 3 2 1 4 0 4 1 2 3 2 4 0 | Rezolvare |
| #455. [2013-04-26 - 09:26:24] Se da un arbore cu n varfuri prin vectorul TATA. Afisati care dintre varfurile arborelui por fi alese ca radacina a acestuia astfel incat arborele sa aiba inaltime minima. Exemplu: date.in 6 2 0 2 1 3 1 date.out 2 | Rezolvare |
| #453. [2013-04-20 - 08:34:54] Arbore partial de cost minim (cu algoritmul lui Prim). Exemplu: date.in 5 8 1 2 3 1 3 2 1 5 4 1 4 3 2 3 6 3 4 1 3 5 1 4 5 1 date.out 1 3 2 3 4 1 3 5 1 1 2 3 *solutia nu este unica | Rezolvare |
| #452. [2013-04-20 - 08:25:16] Arbore partial de cost minim (cu algoritmul lui Kruskal). Exemplu: date.in 5 8 1 2 3 1 3 2 1 5 4 1 4 3 2 3 6 3 4 1 3 5 1 4 5 1 date.out 3 4 1 3 5 1 1 3 2 1 2 3 *solutia nu este unica | Rezolvare |
| #337. [2011-02-20 - 22:32:00] Din fisierul sd.in se citeste un numar natural n reprezentand numarul de varfuri ale unui arbore binar si apoi vectorii S si D pentru descendentii fiecarui nod din arbore. a) Sa se parcurga arborele in preordine, inordine si postordine. b) Sa se parcurga arborele pe nivele c) Sa se calculeze si sa se afiseze inaltimea arborelui. Exemplu: sd.in 7 2 4 0 0 7 0 0 3 5 6 0 0 0 0 Se va afisa: Preordine: 1 2 4 5 7 3 6 Inordine: 4 2 7 5 1 3 6 Postordine: 4 7 5 2 6 3 1 Pe nivele: 1 2 3 4 5 6 7 Adancimea: 3 | Rezolvare |
| #41. [2009-03-15 - 22:09:29] Se citeste un arbore prin vectorul de tati. Sa se determine si sa se afiseze cel mai lung lant din arbore. Ex: Pentru vectorul de tati 2 0 2 5 2 5 3 7 se afiseaza lantul 4 5 2 3 7 8 |  | Rezolvare |
| #39. [2009-03-15 - 21:41:14] Se citeste o padure cu n varfuri prin vectorul de tati. Sa se determine din cati arbori este formata padurea. Ex: Pentru vectorul de tati 2 0 2 0 4 5 0 7, padurea este formata 3 arbori. |  | Rezolvare |
| #37. [2009-03-12 - 22:55:17] Se citeste un arbore cu n varfuri dat prin vectorul TATA si apoi un varf k. Sa se afiseze vectorul TATA obtinut prin mutarea radacinii arborelui in varful k. Ex: Pentru vectorul de tati 2 0 2 1 3 si nodul k=5 se va afisa vectorul 2 3 5 1 0. | 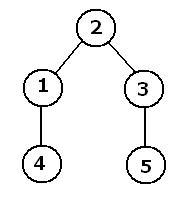 | Rezolvare |
| #36. [2009-03-12 - 22:41:49] Ce citeste un graf neorientat cu n varfuri si m muchii etichetate prin costuri (ponderi) pozitive. Graful este dat prin vectorul muchiilor. Se cere sa se determine un arbore partial de cost minim (are suma costurilor muchiilor sale minima). | Rezolvare |
| #6. [2009-03-07 - 21:17:18] Se citeste un arbore cu n varfuri dat prin vectorul TATA. a) Sa se afiseze gradele varfurilor. b) Sa se afiseze pentru fiecare varf nivelul pe care se afla (numerotarea nivelelor incepe de la 0-radacina). Ex: Pentru vectorul de tati 2 0 2 1 3 se vor afisa urmatorii vectori: Gradele: 2 2 2 1 1 Nivelele: 1 0 1 2 2 |  | Rezolvare |
| #4. [2009-03-05 - 21:26:50] Se citeste un arbore cu n varfuri dat prin vectorul TATA. Sa se afiseze frunzele arborelui. Ex: Pentru vectorul de tati 2 0 2 1 3 se vor afisa frunzele 4 si 5. |  | Rezolvare |
| #3. [2009-03-05 - 21:24:40] Se citeste un arbore cu n varfuri dat prin vectorul muchiilor si apoi se citeste varful radacina. Sa se calculeze si sa se afiseze numarul de niveluri ale arborelui. Ex: Pentru un arbore cu 5 noduri si muchiile [1,2] [2,3] [1,4] [3,5] numarul de niveluri este 3. |  | Rezolvare |
| #2. [2009-02-27 - 22:41:42] Se citeste un arbore cu n varfuri dat prin vectorul muchiilor si apoi se citeste varful radacina. Sa se construiasca si sa se afiseze vectorul TATA. Ex: Pentru un arbore cu 5 noduri, cu muchiile [1,2] [2,3] [1,4] [3,5] si radacina 2 se obtine vectorul de tati 2 0 2 1 3 |  | Rezolvare |
| #1. [2009-02-27 - 19:39:12] Se citeste un arbore cu n varfuri dat prin vectorul TATA. a) Sa se afiseze muchiile arborelui b) Sa se construiasca si sa se afiseze matricea de adiacenta a arborelui. Ex: Pentru vectorul de tati 2 0 2 1 3 se vor afisa muchiile [1,2] [2,3] [1,4] [3,5] si matricea de adiacenta 0 1 0 1 0 1 0 1 0 0 0 1 0 0 1 1 0 0 0 0 0 0 1 0 0 |  | Rezolvare |
12 ian 2026
Site-ul conține 884 de probleme rezolvate
Copyright © 2009-2018 Muresan Vasile Ciprian