Backtracking
| #874. [2018-12-11 - 17:19:53] Se dá un numár natural s cu cel mult 9 cifre. AfiàaéÈi, ûÛn ordine lexicograficá, toate modalitáéÈile de a-l scrie pe s ca produs de divizori proprii distincài ai lui s. Exemplu: 30 poate fi scris in urmátoarele moduri: 2 3 5 2 15 3 10 5 6 | Rezolvare |
| #837. [2017-10-21 - 14:44:34] Se citeste un cuvant format din maxim 10 litere mici distincte. Afisati in ordine lexicografica toate anagramele cuvantului citit care au proprietatea ca nu contin doua vocale alaturate si nici doua consoane alaturate (practic vocalele si consoanele trebuie sa alterneze). Daca acest lucru nu este posibil se va afisa mesajul IMPOSIBIL. Exemplu: Daca s="cosmina" anagramele vor fi: caminos camison camonis ... sonimac Daca s="cosmin" se va afisa IMPOSIBIL | Rezolvare |
| #834. [2017-10-04 - 08:45:57] Se da un numar natural n (n<=5) si 2*n numere naturale cu cel mult 3 cifre fiecare reprezentand inaltimile in centimetri a 2*n soldati. Sa se aranjeze soldatii pe doua randuri a cate n soldati fiecare astfel incat fiecare soldat inafara de primul de pe rand sa aiba in stanga un soldat mai inalt decat el si fiecare soldat de pe randul 2 sa aiba in fata un soldat mai inalt decat el. Exemplu: 3 183 180 169 195 193 184 Aranjarile posibie sunt: 195 193 184 183 180 169 195 193 183 184 180 169 195 193 180 184 183 169 195 184 183 193 180 169 195 184 180 193 183 169 | Rezolvare |
| #818. [2016-12-16 - 09:46:29] Se citesc din fisierul fazan.in numerele naturale n, si m (n<=15, m<=n) si apoi n cuvinte distincte cu cel mult 10 litere fiecare. Sa se afiseze toate secvente de cate m cuvinte dintre cele citite care sa respecte conditiile jocului "fazan". Exemplu: fazan.in 8 3 paul alina asfalt nas ultim imagine nasture real fazan.out paul ultim imagine alina nas asfalt alina nasture real nasture real alina real alina nas real alina nasture | Rezolvare |
| #817. [2016-12-16 - 09:35:56] Se citesc din fisierul kp.in numerele naturale n,k,p (n<=20, k<=n, p<=1000) si apoi n numere naturale distincte cu cel mult 5 cifre fiecare, reprezentand elementele unei multimi A. Numim submultime "kp" o submultime cu k elemente a multimii A care sa aiba cmmdc al elementor cel putin egal cu p. De exemplu, submultimea {6,9,15} este submultime "33" (adica are 3 elemente si cmmdc-ul lor este cel putin 3), dar nu este submultime "34" si nici "52". Sa se afiseze toate submultime "kp" ale multimii A. Exemplu: kp.in 7 3 5 3 6 9 15 20 24 30 kp.out 6 24 30 15 20 30 Ambele submultimi au cate 3 elemente si cmmdc al elementelor cel putin egal cu 5 (prima are 6, iar a doua 5) | Rezolvare |
| #812. [2016-10-20 - 11:09:01] pbinfo.ro -> CifreGen5 | Rezolvare |
| #811. [2016-10-20 - 11:03:11] Se citesc numerele naturale n,a,b,p,q (n<=20, a<=b<=n, p<=q) si apoi n punctaje diferite ale unor intrebari. Sa se afiseze toate modurile in care se poate alege pentru un test un numar de intrebari cuprins intre a si b si care sa aiba punctajul total intre p si q. Exemplu: 7 4 5 20 25 6 5 7 8 2 3 10 se vor afisa 6 5 7 2 6 5 7 2 3 6 5 7 3 6 5 8 2 6 5 8 2 3 .... 8 2 3 10 | Rezolvare |
| #810. [2016-10-20 - 10:50:28] Se citesc doua numere naturale n si s (n<=10, s<=20). Afisati Ÿn ordine crescatoare toate numerele cu n cifre care au suma cifrelor egala cu s si Ÿn care oricare doua cifre alaturate au paritate diferita. Exemple: n=4, s=8 => 1016, 1034, 1052, 1070, 1214, 1232, 7010 | Rezolvare |
| #809. [2016-10-20 - 10:46:17] Se citesc un cuvãnt s (cu cel mult 10 caractere litere mici distincte). Sa se genereze si sa se afiseze toate anagramele cuvãntului s Ÿn care consoanele sunt puncte fixe. Exemplu: s=alinus, => alinus, alunis, ilanus, ilunas, ulanis, ulinas. | Rezolvare |
| #808. [2016-10-20 - 10:43:37] Se citesc doua numere naturale n si m (n,m<=10) si apoi o multime A cu n elemente naturale ordonate crescator. Afisati Ÿn ordine lexicografica toate submultimile cu m elemente ele multimii A Ÿn care nu exista doua elemente pare alaturate. Daca problema nu are solutie, se va afisa mesajul NU EXISTA. Exemple: n=5, m=3 si A={1,4,6,7,9} => {1, 4, 7} {1,4,9}, {1,6,7}, {1,6,9}... n=4, m=3 si A={1,4,6,8} =>NU EXISTA | Rezolvare |
| #807. [2016-10-20 - 10:40:29] Se citesc doua numere naturale n si s (n<=10, s<=20). Afisati Ÿn ordine crescatoare toate numerele cu n cifre distincte care au suma cifrelor egala cu s. Daca problema nu are solutie, se va afisa mesajul NU EXISTA. Exemple: n=4, s=9 => 1026, 1035, 1053, 1062, 1206, 1260, 1305 n=4, s=5 =>NU EXISTA | Rezolvare |
| #806. [2016-10-20 - 10:38:01] Se citesc un cuvãnt s (cu cel mult 10 caractere litere mici distincte) si un numar natural n (n<=10). Sa se genereze si sa se afiseze toate cuvintele care se pot obtine din s eliminãnd exact n litere. Exemplu: s=cosmin, n=4 =>co, cs, cm, ci, cn, os, om in | Rezolvare |
| #805. [2016-10-20 - 10:25:33] Se citeste un numar natural n (n<10) si apoi o multime A cu n elemente naturale ordonate crescator. Afisati Ÿn ordine lexicografica toate permutarile multimii A Ÿn care elementele pare sunt puncte fixe. Exemplu: n=5 si A={1,4,6,7,9} => se vor genera permutarile Ÿn care 4 si 6 nu Ÿsi modifica pozitia (6 solutii). | Rezolvare |
| #778. [2016-03-08 - 16:29:17] Scrieti un program care afiseaza in fisierul cercuri.out toate modalitatitile de inlocuire a literelor din imaginea alaturata cu cifre de la 1 la 9 astfel incat suma cifrelor din fiecare cerc sa fie aceeasi. | 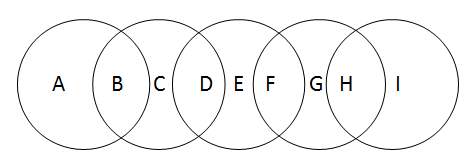 | Rezolvare |
| #647. [2014-11-15 - 12:40:28] Hercule trebuie sa strabata un labirint cu capcane reprezentat de o matrice nXn. Pentru fiecare celula a labirintului, se cunoaste timpul in minute dupa care celula respectiva devine capcana. Dupa ce o celula devine capcana, Hercule moare daca intra in acea celula. Hercule porneste din coltul stanga-sus al labirintului si trebuie sa ajunga in coltul dreapta jos. El are nevoie de un minut ca sa treaca dintr-o celula intr-una vecina si se poate deplasa in sus, in jos, spre stanga sau spre dreapta. Sa se afiseze timpul minim in care poate Hercule sa strabata labirintul, numarul de drumuri de timp minim, precum si toate drumurile minime pe care le poate urma Hercule prin labirint de la intrare la iesire, astfel incat Hercule sa nu moara. Drumurile vor fi afisate ca matrici in care sunt indicati pasii lui Hercule. Exemplu: hercule.in 6 6 3 4 5 6 7 8 3 1 1 1 1 9 5 6 7 12 11 10 1 7 1 13 1 1 1 8 1 14 15 16 1 9 10 11 12 17 hercule.out 11 4 1 0 0 0 0 0 2 0 0 0 0 0 3 4 5 6 0 0 0 0 0 7 0 0 0 0 0 8 9 10 0 0 0 0 0 11 1 0 0 0 0 0 2 0 0 0 0 0 3 4 5 6 0 0 0 0 0 7 0 0 0 0 0 8 9 0 0 0 0 0 10 11 1 0 0 0 0 0 2 0 0 0 0 0 3 4 5 6 0 0 0 0 0 7 0 0 0 0 0 8 0 0 0 0 0 9 10 11 1 0 0 0 0 0 2 0 0 0 0 0 3 4 0 0 0 0 0 5 0 0 0 0 0 6 0 0 0 0 0 7 8 9 10 11 | Rezolvare |
| #631. [2014-10-06 - 22:35:52] Se citeste un numar natural n. Generati si afisati toate combinatiile de cate n cifre binare care nu au doua cifre de 1 alaturate. Exemplu: n=3 combinatiile sunt: 0 0 0 0 0 1 0 1 0 1 0 0 1 0 1 | Rezolvare |
| #620. [2014-10-03 - 22:20:03] Sa se afiseze in ordine alfabetica anagramele unui cuvant format din litere distincte. Exemplu: date.in rac date.out acr arc car cra rac rca | Rezolvare |
| #616. [2014-10-03 - 21:35:31] Se citesc n numere naturale. Determinati o aranjare a acestor numere sub forma unui cerc, astfel incat suma produselor de cate doua numere alaturate sa fie maxima. Exemplu: date.in 6 1 8 3 2 5 4 date.out 1 2 4 8 5 3 | Rezolvare |
| #551. [2014-02-11 - 08:24:51] Se citeste un numar natural n si apoi o multime cu n elemente numere naturale. Folosind interschimbari de elemente generati si afisati permutarile multimii citite. | Rezolvare |
| #511. [2013-11-26 - 18:18:09] Se citeste un numar natural n. Afisati permutarile multimii 1,2,3...n in care elementele pare sunt puncte fixe (se afla pe pozitie egale cu valoarea lor). Exemplu: n=5 permutarile care respecta conditia sunt: 1 2 3 4 5 1 2 5 4 3 3 2 1 4 5 3 2 5 4 1 5 2 1 4 3 5 2 3 4 1 (2 si 4 sunt puncte fixe) | Rezolvare |
| #510. [2013-11-26 - 18:14:03] Se citeste un numar natural n. Afisati permutarile multimii 1,2,3...n in care pana la jumatate elementele sunt in ordine descrescatoare, iar de la jumatate pana la final in ordine crescatoare. Exemplu: n=5 permutarile care respecta conditia sunt: 3 2 1 4 5 4 2 1 3 5 4 3 1 2 5 5 2 1 3 4 5 3 1 2 4 5 4 1 2 3 | Rezolvare |
| #505. [2013-11-13 - 19:34:53] Se citesc doua numere naturale n si k, k fiind mai mic decat numarul de cifre ale numarului n. Afisati cel mai mare numar care se poate forma eliminand k cifre din numarul n. Exemplu: n=3452234 k=4 numarul cautat este 534 | Rezolvare |
| #504. [2013-11-13 - 19:34:44] Se citesc doua numere naturale n si k. Generati si afisati toate toate numerele naturale formate din n cifre care contin exact k cifre de 1. | Rezolvare |
| #397. [2012-11-28 - 09:00:31] Pe o tabla de sah nXn sunt plasate marcate prin valoarea -1, iar prin valoarea 0 sunt marcate pozitiile libere. Intr-o pozitie jo de pe prima linie se afla un pion. a) Determinati toate traseele pe care poate ajunge pionul pana pe ultima linie. b) Determinati traseul pe care pionul ia numar maxim de piese. Traseele vor fi afisate ca matrice de pasi. Exemplu: Intrare: 5 0 0 0 0 0 0 0 0 0 0 0 -1 0 -1 0 -1 -1 0 0 0 0 0 0 0 0 3 Iesire: 0 0 1 0 0 0 0 2 0 0 0 # 3 # 0 # 4 0 0 0 0 5 0 0 0 0 0 1 0 0 0 0 2 0 0 0 # 3 # 0 # # 4 0 0 0 0 5 0 0 0 0 1 0 0 0 0 2 0 0 0 # 0 3 0 # # 0 4 0 0 0 0 5 0 ia maxim2 piese si solutia este 0 0 1 0 0 0 0 2 0 0 0 3 0 # 0 4 # 0 0 0 5 0 0 0 0 | Rezolvare |
| #391. [2012-11-16 - 11:45:15] Se citeste o matrice a cu n linii si m coloane care contine numere naturale. Afisati toate modurile in care se poate parcurge matricea mergand in vecinii de sus, jos, stanga si dreapta astfel incat prin fiecare element sa se treaca de atatea ori cat este valoarea lui. Solutiile se vor afisa ca succesiune de pozitii si ca succesiune de directii. Exemplu: date.in 4 4 0 1 0 0 1 2 0 1 0 1 1 2 0 0 1 1 date.out 1,2 2,2 2,1 2,2 3,2 3,3 4,3 4,4 3,4 2,4 3,4 SVESESENNS 1,2 2,2 2,1 2,2 3,2 3,3 3,4 2,4 3,4 4,4 4,3 SVESEENSSV 2,1 2,2 1,2 2,2 3,2 3,3 4,3 4,4 3,4 2,4 3,4 ENSSESENNS 2,1 2,2 1,2 2,2 3,2 3,3 3,4 2,4 3,4 4,4 4,3 ENSSEENSSV 3,4 2,4 3,4 4,4 4,3 3,3 3,2 2,2 1,2 2,2 2,1 NSSVNVNNSV 3,4 2,4 3,4 4,4 4,3 3,3 3,2 2,2 2,1 2,2 1,2 NSSVNVNVEN 4,3 4,4 3,4 2,4 3,4 3,3 3,2 2,2 1,2 2,2 2,1 ENNSVVNNSV 4,3 4,4 3,4 2,4 3,4 3,3 3,2 2,2 2,1 2,2 1,2 ENNSVVNVEN | Rezolvare |
| #390. [2012-11-15 - 11:47:02] Se dau n punct in plan prin coordonatele lor. Gasiti cel mai mare patrat care se poate forma cu varfurile in 4 dintre punctele citite. date.in: 9 1 3 0 0 1 1 1 0 0 1 3 5 5 1 5 6 0 6 date.out: 0,1 5,1 5,6 0,6 | Rezolvare |
| #389. [2012-11-15 - 09:40:24] Magazinul PetShop vinde n specii de pesti despre care se stiu m perechi de pesti care nu pot fi pusi in acelasi acvariu deoarece se ataca. Gigi are un acvariu si vrea sa isi cumpere un numar maxim de specii de pesti de la magazinul PetShop. Ajutati-l pe Gigi sa aleaga speciile de pesti astfel incat sa poata avea un numar maxim de specii in acvariul sau. Exemplu: n=6, m=5 perechile: 1 2 1 3 1 4 3 5 3 6 solutia: 2 4 5 6 | Rezolvare |
| #388. [2012-11-15 - 09:12:27] Pe n scaune sunt aranjate n persoane intr-o ordine precizata. Sa se rearanjeze in toate modurile cele n persoane pe cele n scaune tinand cont de urmatoarele doua conditii: - doua persoane alaturate trebuie sa nu fi fost alaturate in aranjarea initiala - fiecare persoana trebuie sa stea pe un scaun diferit de cel pe care a stat initial Exemplu: n=6 aranjarea initiala 6 2 3 4 5 1 rezultate: 1 3 5 2 4 6 1 3 5 6 4 2 1 3 6 5 2 4 1 4 2 5 3 6 1 4 2 5 6 3 2 1 4 6 3 5 ... 5 6 4 2 1 3 | Rezolvare |
| #387. [2012-11-14 - 10:16:31] Un patrat de latura n este numit magic daca este format din numerele de la 1 la n*n si suma pe fiecare linie, pe fiecare coloana, precum si pe cele 2 diagonale este constanta. Exemplu: 2 7 6 9 5 1 4 3 8 | Rezolvare |
| #386. [2012-11-09 - 09:30:39] Se citeste un numar natural n (cel mult 4). Afisati toate matricile n*n care contin elementele distincte de la 1 la n*n si in care orice element are paritate diferita de orice vecin al sau (vecinii se considera pe linie si pe coloana). Exemplu: 1 2 3 4 6 5 8 7 9 10 11 14 12 13 16 15 | Rezolvare |
| #385. [2012-11-09 - 08:33:08] Se citeste o matrice nXm care contine litere mici. Gasiti cel mai lung sir format numai din vocale care se poate construi cu literele din matrice prin deplasare paralela cu liniile si coloanele matricii, fara a trece de mai multe ori prin aceeasi litera. Exemplu: date.in 6 6 lptxkh yaioua ttbucx iokexe nuaexi mptxuo date.out aioueeauoi | Rezolvare |
| #384. [2012-11-09 - 08:30:11] Se considera n piese de domino citite ca perechi de numere naturale, fiecare pe cate un rand de intrare. Se citeste apoi un numar natural a. Sa se afiseze cel mai lung lant domino care se poate forma cu piesele date, fara a roti piesele. (Un lant domino se alcatuieste din piese domino astfel incat o piesa este urmata de alta a carei prima jumatate coincide cu jumatatea a doua a piesei curente.) Ex: 1,2 2,6 6,8 date.in: 6 1 2 1 3 3 4 2 3 3 5 4 5 date.out: 1 2 2 3 3 4 4 5 | Rezolvare |
| #383. [2012-11-07 - 11:44:39] Se considera n piese de domino citite ca perechi de numere naturale, fiecare pe cate un rand de intrare. Se citeste apoi un numar natural a. Sa se afiseze toate solutiile de aranjare a acestor piese intr-un lant domino de lungime a, cu posibilitatea de a roti piesele. (Un lant domino se alcatuieste din piese domino astfel incat o piesa este urmata de alta a carei prima jumatate coincide cu jumatatea a doua a piesei curente.) Ex: 1,2 2,6 6,8 date.in: 6 1 2 1 3 3 4 2 3 3 5 4 5 3 date.out: 1 2 2 3 3 1 1 2 2 3 3 4 1 2 2 3 3 5 2 1 1 3 3 4 2 1 1 3 3 2 2 1 1 3 3 5 ... 5 4 4 3 3 2 5 4 4 3 3 5 | Rezolvare |
| #382. [2012-11-07 - 10:59:14] Se considera n piese de domino citite ca perechi de numere naturale, fiecare pe cate un rand de intrare. Se citeste apoi un numar natural a. Sa se afiseze toate solutiile de aranjare a acestor piese intr-un lant domino de lungime a, fara a roti piesele. (Un lant domino se alcatuieste din piese domino astfel incat o piesa este urmata de alta a carei prima jumatate coincide cu jumatatea a doua a piesei curente.) Ex: 1,2 2,6 6,8 date.in: 6 1 2 1 3 3 4 2 3 3 5 4 5 3 date.out: 1 2 2 3 3 4 1 2 2 3 3 5 1 3 3 4 4 5 2 3 3 4 4 5 | Rezolvare |
| #381. [2012-11-01 - 08:14:56] Un labirint se codifica printr-o matrice nXm in care 0 sunt pozitii libere, iar -1 reprezinta zidurile. In pozitia io,jo se afla un soricel care se poate deplasa pe patru directii paralele cu liniile si coloanele matricii. Afisati cel mai scurt drum prin care soricelul poate parasi labirintul. Ex: date.in 6 5 -1 -1 -1 -1 -1 0 0 0 0 -1 -1 0 -1 0 -1 0 0 0 0 -1 -1 -1 -1 0 -1 -1 -1 -1 0 -1 3 4 date.out -1 -1 -1 -1 -1 0 0 0 0 -1 -1 0 -1 1 -1 0 0 0 2 -1 -1 -1 -1 3 -1 -1 -1 -1 4 -1 3,4 4,4 5,4 6,4 SSS | Rezolvare |
| #380. [2012-10-31 - 11:40:46] Un munte este memorat ca o matrice n*m in care fiecare pozitie reprezinta altitudinea din acel loc. Intr-o pozitie i0, j0 se afla un alpinist care se poate deplasa in toate cele 8 directii in pozitiile alaturate care au altitudinea cu cel mult 1 mai mare decat cea pe care se afla alpinistul. Stiind ca exista o singura valoare maxima in matrice si ea reprezinta altitudinea varfului muntelui, gasiti toate drumurile pe care alpinistul poate ajunge in varf fara a trece de 2 ori prin aceeasi pozitie. Solutiile se vor afisa ca matrice si ca sir de cordonate. Ex: date.in 4 4 1 1 1 1 1 1 1 5 6 7 6 4 5 4 3 2 4 4 date.out 0 0 0 0 0 0 0 4 0 6 5 3 0 0 2 1 4,4 4,3 3,4 2,4 3,3 3,2 0 0 0 0 0 0 0 4 8 9 5 3 7 6 2 1 4,4 4,3 3,4 2,4 3,3 4,2 4,1 3,1 3,2 0 0 0 0 0 0 0 0 5 6 0 0 4 3 2 1 4,4 4,3 4,2 4,1 3,1 3,2 | Rezolvare |
| #379. [2012-10-26 - 12:40:49] Se citesc doua numere naturale n si m (m mai mic decat n). Afisati toate partitiile multimii {1,2,3, ... , n} care sunt formate din m submultimi. Exemplu: n=4 m=3 Se vor afisa partitiile: {1 2 } {3 } {4 } {1 3 } {2 } {4 } {1 } {2 3 } {4 } {1 4 } {2 } {3 } {1 } {2 4 } {3 } {1 } {2 } {3 4 } | Rezolvare |
| #378. [2012-10-26 - 08:30:05] Un student are de dat n examene numerotate de la 1 la n intr-o sesiune formata din m zile (m este cel putin de 2 ori mai mare decat n). Afisati toate modurile in care isi poate programa studentul examenele astfel incat sa nu dea 2 examene in zile consecutive si sa dea examenele in ordine de la 1 la n. Ex: n=3 m=6 Solutii: 010203 100203 102003 102030 (0 codifica zilele libere) | Rezolvare |
| #371. [2012-10-19 - 08:36:56] Se dau in plan n puncte albe si n puncte negre prin coordonatele lor intregi. Fiecare punct alb trebuie unit cu un singur punct negru pentru a forma in acest fel n segmente. Se cere sa se realizele n segmente care sa nu se intersecteze, fiecare segment avand o extremitate un punct alb si cealalta un punct negru. Exemplu: Pentru datele de intrare: 3 1 1 1 2 1 3 3 1 3 3 3 2 Se obtine segmentele: (1,1)-(3,1) (1,2)-(3,2) (1,3)-(3,3) | Rezolvare |
| #369. [2012-10-18 - 13:24:01] Un student are in sesiune n examene fiecare avand asociat un numar de credite. Pentru a promova sesiunea el trebuie sa acumuleze cel putin s credite. Gasiti toate nodurile in care poate el sa isi aleaga examenele pentru a promova sesiunea astfel incat sa faca un efort minim, adica sa nu mearga la examene fara de care oricum promoveaza. Ordinea examenelor nu este importanta, iar daca studentul isi aleage un examen se considera ca il promoveaza. Ex: n=6 creditele: 7 8 10 10 2 6 s=30 Solutii: 10 10 8 7 10 10 8 6 10 10 8 2 10 10 7 6 10 8 7 6 10 8 7 6 (se repeta deoarece poate alege oricare din cele 2 examene cu 10 credite) | Rezolvare |
| #368. [2012-10-17 - 10:24:37] Se citeste un numar natural n si apoi n numere naturale ordonate strict crescator reprezentand valorile a n bancnote. Se citeste apoi o suma de bani s si se cere sa se plateasca in toate modurile posibile suma s cu bancnote de valorile precizate folosind cel putin o bancnota de fiecare valoare data. Se presupune ca avem la dispozitie oricate bancnote de fiecare valoare. Ex: n=4 valorile bancnotelor: 1 5 10 50 s=100 Se vor obtine solutii de forma: 15*1 1*5 3*10 1*50 15*1 3*5 2*10 1*50 15*1 5*5 1*10 1*50 | Rezolvare |
| #366. [2012-10-17 - 10:24:24] Se citeste un numar natural n si apoi n numere naturale ordonate strict crescator reprezentand valorile a n bancnote. Se citeste apoi o suma de bani s si se cere sa se plateasca in toate modurile posibile suma s cu bancnote de valorile precizate. Se presupune ca avem la dispozitie oricate bancnote de fiecare valoare. Ex: n=4 valorile bancnotelor: 1 5 10 50 s=100 Se vor obtine solutii de forma: 2*50 5*10 1*50 10*10 2*5 4*10 1*50 ... 35*1 1*5 1*10 1*50 ... 95*1 1*5 100*1 | Rezolvare |
| #364. [2012-10-10 - 10:23:31] Se citeste un numar natural n. Afisati toate numerele formate din n cifre in care oricare doua cifre alaturate au paritate diferita. Ex. Pentru n=4 se vor obtine: 1010 1012 1014 ... 2101 2103 ... 9898 | Rezolvare |
| #363. [2012-10-10 - 09:08:06] Se dau urmatoarele 6 culori: alb, galben, rosu, verde, albastru si negru. Costruiti toate steagurile formate din 3 culori care indeplinesc urmatoarele conditii: - orice steag trebuie sa contina culoarea verde sau culoarea galben la mijloc. - culorile din fiecare steag trebuie sa fie distincte. | Rezolvare |
| #362. [2012-10-04 - 14:24:56] La curtea regelui Arthur s-au adunat n cavaleri numerotati de la 1 la n. Despre ei se cunosc relatii de dusmanie de forma (x,y) cu semnificati ca x si y se dusmanesc. Afisati toate modurile in care Arthur ii poate aranja la o masa rotunda cu n scaune astfel incat sa nu stea unul langa altul 2 cavaleri care dusmanesc. | Rezolvare |
| #282. [2010-11-21 - 16:36:22] Harta unui oras este codificata ca o matrice nXm in care 0 reprezinta pozitie accesibila (strada) si -1 reprezinta pozitie inaccesibila (clarire, zid). In pozitia ir,jr se afla Romeo, iar in pozitia ij,jj se afla Julieta. Romeo se poate deplasa pe pozitii cu laloarea 0, alaturate pe linii si coloane cu pozitia curenta, fara sa treaca de doua ori prin aceeasi pozitie. Determinati si afisati cel mai scurt traseu pe care poate ajunge romeo la Julieta. Solutia se va afisa prin pasi marcari in matrice si ca sir de coordonate prin care trece Romeo. Toate datele se citesc din fisierul rj.in, iar solutia se afiseaza in fisierul rj.out. Exemplu: Pentru datele de intrare: 5 7 -1 -1 0 -1 -1 -1 -1 -1 0 0 0 0 0 0 -1 0 -1 -1 -1 0 -1 -1 0 0 0 0 0 0 -1 -1 -1 -1 -1 -1 -1 2 2 3 6 solutia este: -1 -1 0 -1 -1 -1 -1 -1 1 2 3 4 5 0 -1 0 -1 -1 -1 6 -1 -1 0 0 0 0 0 0 -1 -1 -1 -1 -1 -1 -1 2,2 2,3 2,4 2,5 2,6 3,6 | Rezolvare |
| #274. [2010-11-04 - 09:47:12] Pe o tabla de sah nXn sunt plasate marcate prin valoarea 1, iar prin valoarea 0 sunt marcate pozitiile libere. Intr-o pozitie j0 de pe prima linie se afla un pion. Determinati toate traseele pe care poate ajunge pionul pana pe ultima linie. Traseele vor fi afisate atat in matrice cat si ca sir de pozitii. Exemplu: pentru datele 5 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0 3 exista 3 solutii marcate in matrice: 0 0 0 0 0 0 0 1 0 0 0 0 2 0 0 0 1 3 1 0 0 0 4 0 0 sau 0 0 0 0 0 0 0 1 0 0 0 0 2 0 0 0 3 0 1 0 0 4 0 0 0 sau 0 0 0 0 0 0 0 1 0 0 0 0 2 0 0 0 1 0 3 0 0 0 0 4 0 | Rezolvare |
| #273. [2010-11-01 - 11:45:51] Se citeste o matrice nXm care contine litere mici si apoi un cuvant s. Gasiti cel mai lung prefix al cuvantului s care se poate construi cu literele din matrice prin deplasare paralela cu liniile si coloanele matricii putand trece de mai multe ori prin aceeasi litera. Exemplu: 5 6 axsads ccnama nnuair asdydi sedrft anamariana prefixul este anamaria | Rezolvare |
| #272. [2010-11-01 - 11:45:45] Se citeste o matrice nXm care contine litere mici si apoi un cuvant s. Gasiti cel mai lung prefix al cuvantului s care se poate construi cu literele din matrice prin deplasare paralela cu liniile si coloanele matricii fara a trece de doua ori prin aceeasi litera. Exemplu: 5 6 axsads aanama nnaair asdydi sedrft anamariana prefixul este anamaria | Rezolvare |
| #271. [2010-11-01 - 10:49:04] Se citeste o matrice nXm cu elemente numere naturale si o pozitie io, jo din matrice in care se afla un robot care se poate deplasa paralel cu liniile si coloanele matricii pe pozitii alturate. Afisati toate drumurile pe care poate parcurge robotul matricea trecand prin fiecare pozitie de atatea ori cat este valoarea pozitiei respective. Drumurile vor fi afisate ca perechi de coordonate. Exemplu: pentru datele de intrare 6 7 0 0 0 0 0 0 0 0 0 1 1 1 0 0 0 1 2 0 2 1 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 2 se afiseaza 3,2 3,3 4,3 3,3 2,3 2,4 2,5 3,5 4,5 3,5 3,6 3,2 3,3 4,3 3,3 2,3 2,4 2,5 3,5 3,6 3,5 4,5 | Rezolvare |
| #251. [2010-10-25 - 11:21:23] Un labirint se codifica printr-o matrice nXm in care 0 sunt pozitii libere, iar -1 reprezinta zidurile. In pozitia io,jo se afla un soricel care se poate deplasa pe patru directii paralele cu liniile si coloanele matricii. Afisati toate drumurile prin care soricelul poate parasi labirintul. Exemplu: 5 7 -1 -1 0 -1 -1 -1 -1 0 0 0 0 0 0 0 -1 -1 -1 -1 -1 0 -1 -1 0 0 0 0 0 0 -1 -1 -1 -1 -1 -1 -1 4 2 O solutie este: -1 -1 0 -1 -1 -1 -1 0 0 0 0 0 7 8 -1 -1 -1 -1 -1 6 -1 -1 1 2 3 4 5 0 -1 -1 -1 -1 -1 -1 -1 4,2 4,3 4,4 4,5 4,6 3,6 2,6 2,7 | Rezolvare |
| #250. [2010-10-21 - 12:40:03] Se citeste un numar natural n si apoi n culori distincte date ca siruri de caractere. Afisati toate steagurile care se pot forma cu cate 3 culori diferite. | Rezolvare |
| #249. [2010-10-21 - 12:39:55] Se citeste un numar natural n. Sa se afiseze toate modurile in care poate fi descompus ca suma de numere naturale impare distincte. | Rezolvare |
| #248. [2010-10-21 - 12:39:47] Se citeste un numar natural n. Sa se afiseze toate modurile in care poate fi descompus ca produs de numere naturale diferite de 1 si n. Exemplu: 36 poate fi descompus ca: 2*2*3*3 2*2*9 2*18 3*3*4 ..... | Rezolvare |
| #232. [2010-10-14 - 09:36:47] Se citeste un numar natural n si apoi n bancnote cu valorile v1, v2, ..., vn. Se citeste apoi o suma de bani s. Afisati toate modurile in care poate fi platita suma s folosind cel putin cate o bancnota de fiecare valoare. | Rezolvare |
| #214. [2010-03-20 - 18:00:07] Se citeste un cuvant format doar din litere mici distincte. Sa se genereze anagramele lui. | Rezolvare |
| #213. [2010-03-20 - 17:59:51] Sa se afiseze toate numerele naturale formate doar din cifre impare distincte, sa se calculeze suma si numarul acestora. | Rezolvare |
| #212. [2010-03-20 - 17:59:38] Sa se genereze toate numerele formate din 5 cifre impare distincte. | Rezolvare |
| #211. [2010-03-20 - 17:59:24] Se citeste un numar natural n si un numar natural p mai mic decat n. Sa se descompuna n in toate modurile ca suma de p numere naturale. | Rezolvare |
| #210. [2010-03-20 - 17:59:11] Sa se aranjeze in toate modurile n pisici si m caini astfel incat nicio pisica sa nu fie asezata intre 2 caini. | Rezolvare |
| #191. [2010-02-28 - 23:07:11] Sa se genereze si sa numere toate submultimile de cate p elemente ale multimii {1,2,3,...,n}. | Rezolvare |
| #190. [2010-02-28 - 23:07:03] Sa se genereze si sa numere toate aranjamentele de cate p elemente ale multimii {1,2,3,...,n}. | Rezolvare |
| #189. [2010-02-28 - 23:06:53] Sa se genereze si sa numere toate permutarile multimii {1,2,3,...,n}. | Rezolvare |
| #188. [2010-02-28 - 23:06:14] Sa se genereze si sa numere toate submultimile multimii {1,2,3,...,n}. | Rezolvare |
| #187. [2010-02-28 - 23:06:09] Sa se genereze si sa numere toate permutarile multimii {1,2,3,...,n} care au proprietatea ca oricare doua elemente alaturate au paritate diferita. Ex: pentru n=4: 1 2 3 4 1 4 3 2 2 1 4 3 ... 4 3 2 1 | Rezolvare |
| #186. [2010-02-28 - 23:06:01] Sa se genereze si sa numere toate permutarile multimii {1,2,3,...,n} care incep cu valoarea 1. | Rezolvare |
| #185. [2010-02-28 - 23:05:56] Sa se genereze si sa numere toate numerele formate din p cifre distincte avand cifrele ordonate crescator. | Rezolvare |
| #120. [2009-11-24 - 13:21:27] Se citeste un numar natural n. Sa se afiseze in fisierul text cuv.out toate cuvintele de n litere formate doar din litere mici care nu au doua voale alaturate si nici 2 consoane alaturate. | Rezolvare |
| #119. [2009-11-24 - 13:13:41] Se citeste un numar natural n si o permutare a multimii {1,2,...,n}. Sa se afiseze permutarile multimii {1,2,...,n} in care oricare doua elemente alaturate nu au fost alaturate in parmutarea citita. Ex. Pt n= 4 si permutarea 1 2 3 4 , o permutare care respecta regula este 2 4 1 3 | Rezolvare |
| #118. [2009-11-24 - 13:05:42] Sa se afiseze toate permutarile multimii {1,2,...,n} care au proprietatea ca pentru orice element x din permutare (exceptandu-l pe primul) exista un element generat anterior care sa aiba valoare cu unu mai mica sau mai mare ca x. | Rezolvare |
| #115. [2009-11-24 - 12:45:09] Folosind metoda backtracking sa se descompuna in toate modurile un numar natural n ca suma de numere prime distincte ordonate crescator. | Rezolvare |
| #109. [2009-11-21 - 00:22:15] Sa se afiseze in ordine lexicografica submultimile multimii {1,2,...,n}. Ex: pentru n=3 se va afisa: 1 1 2 1 2 3 1 3 2 2 3 3 | Rezolvare |
| #77. [2009-09-29 - 10:10:52] Din fisierul cub.in se citesc de pe prima linie 2 numere naturale n si m si de pe urmatoarele n linii n perechi l si c unde l este lungimea laturii, iar c culoarea pentru n cuburi. l este numar natural, iar c este sir de caractere de lungime maxim 20. Sa se construiasca toate turnurile formate din cel putin m cuburi care se pot forma din cuburile citite din fisier stiind ca un cub se poate pune peste un altul doar daca are latura strict mai mica si culoarea diferita de a celui peste care vrem sa Ÿl punem. Sa se afiseze turnurile obtinute si turnul format din cele mai multe cuburi. Un turn se afiseaza Ÿncepãnd cu cel mai de sus cub. Exemplu: 3 2 3 verde 4 rosu 1 rosu Se obtin turnurile: 1 rosu 3 verde 3 verde 4 rosu si 1 rosu 3 verde 4 rosu | Rezolvare |
| #76. [2009-09-29 - 10:10:46] Folosind metoda backtracking sa se genereze si sa se afiseze Ÿntr-un fisier text toate numerele naturale formate din cifre impare distincte si sa se calculeze suma numerelor astfel generate. | Rezolvare |
| #75. [2009-09-29 - 10:10:40] Se citeste un numar natural n<30. Sa se afiseze toate modalitatile de a-l calcula prin adunari sau scaderi ale numerelor 1,2, ...n. Fiecare numar de la 1 la n va aparea o singura data Ÿn descompunerea lui n. Daca acest lucru nu este posibil, se va afisa mesajul Imposibil. Exemplu: 5=1+2+3+4-5 5=1-2-3+4+5 5=-1+2+3-4+5 | Rezolvare |
| #74. [2009-09-29 - 10:10:34] Se citeste un numar natural n. Sa se afiseze toate modalitatile de a-l descompune ca suma de numere naturale consecutive. Daca acest lucru nu este posibil, se va afisa mesajul Imposibil. Exemplu: Numarul 15 se poate scrie ca urmatoarele sume: 1+2+3+4+5 , 4+5+6 sau 7+8. Numarul 8 nu poate fi scris ca suma de numere consecutive. | Rezolvare |
| #73. [2009-09-29 - 10:02:31] Scrieti un program care citeste de la tastatura un numar natural nenul n (n<=20) si construieste toate numerele formate din n cifre impare cu proprietatea ca oricare doua cifre alaturare dintr-un numar generat sunt consecutive Ÿn multimea cifrelor impare. Exemplu: Pentru n=4 se obtin numere de forma: 1313, 1353, 1357, .... 7979... | Rezolvare |
| #72. [2009-09-29 - 10:02:22] Sa se scrie un program care genereaza si scrie Ÿntr-un fisier toate cuvintele formate din n vocale mici (n numar natural citit de la tastatura, n<10), ordonate alfabetic. De exemplu, pentru n=3 se vor scrie Ÿn fisier: aaa aae aai aao aau aea ..... uuo uuu | Rezolvare |
| #71. [2009-09-29 - 10:02:13] Se citeste de la tastatura un numar natural n par, n<30. Sa se genereze si sa se afiseze pe ecran toate combinatiile de n paranteze rotunde care se Ÿnchid corect. De exemplu, pentru n=4 se obtin urmatoarele combinatii: ( ( ) ) si ( ) ( ) . | Rezolvare |
| #70. [2009-09-29 - 10:02:01] Fiind data o tabla de sah de dimensiunea nxn si un cal Ÿn coltul stãnga sus al acesteia, se cere sa se afiseze toate posibilitatile de mutare a acestei piese de sah astfel Ÿncãt sa treaca o singura data prin fiecare patrat al tablei. O solutie va fi afisata ca o matrice nxn Ÿn care sunt numerotate sariturile calului. Exemplu, pentru n=5, o solutie este 1 14 9 20 23 10 19 22 15 8 5 2 13 24 21 18 11 4 7 16 3 6 17 12 25 | Rezolvare |
| #69. [2009-09-29 - 09:51:44] Fie n>0, natural. Sa se scrie un program care sa afiseze toate partitiile unui numar natural n. Numim partitie a unui numar natural nenul n o multime de numere naturale nenule {p1, p2, , pk} care Ÿndeplinesc conditia p1+p2+ +pk = n. Ex: pt n = 4 programul va afisa: 4 = 1+1+1+1 4 = 1+1+2 4 = 1+3 4 = 2+2 4 = 4 | Rezolvare |
| #48. [2009-03-19 - 15:51:59] Pe o tabla de sah nXn sunt plasate m piese marcate prin valoarea -1, iar prin valoarea 0 sunt marcate pozitiile libere. Intr-o pozitie (i0,j0) se afla un cal, iar intr-o pozitie (i1,j1) un rege. Sa se determine toate traseele pe care calul poate sa mearga din pozitia initiala pana in cea a regelui si sa se intoaca de unde a plecat fara a trece de 2 ori prin aceeasi pozitie si mergand doar pe pozitii libere. Se citesc mai intai n si m, iar apoi m perechi reprezentand coordonatele pieselor. Ultimele se citesc coordonatele calului si ale regelui. Traseele se vor marca intr-o matrice si se for afisa si coordonatele prin care trece calul. | Rezolvare |
| #46. [2009-03-18 - 23:02:23] Se citeste un numar natural n. Sa se afiseze partitiile multimii {1,2,...,n}. | Rezolvare |
| #45. [2009-03-18 - 22:57:12] Sa se scrie un program care reconstituie urmatoarea adunare: CINCI+ | Rezolvare |
| #44. [2009-03-18 - 22:35:39] Pe o tabla de sah nXn sunt plasate m piese marcate prin valoarea -1, iar prin valoarea 0 sunt marcate pozitiile libere. Intr-o pozitie (i0,j0) se afla un cal. Sa se determine traseul format din numar minim de pasi pe care calul poate sa manance toate piesele de pe tabla fara a trece de 2 ori prin aceeasi pozitie. Se citesc mai intai n si m, iar apoi m perechi reprezentand coordonatele pieselor. Ultimele se citesc coordonatele calului. Traseul va fi marcat intr-o matrice care se va afisa. | Rezolvare |
| #5. [2009-03-07 - 21:01:27] Se citeste un numar natural n>=4. Sa se afiseze toate permutarile multimii {1, 2, ... n} care au proprietatea ca diferenta absoluta a oricaror 2 elemente alaturate este cel putin egala cu 2. Ex: Pentru n=4 se obtin permutarile 2 4 1 3 si 3 1 4 2. | Rezolvare |
04 mar 2026
Site-ul conàine 884 de probleme rezolvate
Copyright ôˋ 2009-2018 Muresan Vasile Ciprian